第 1 章 用bookdown 制作电子书
1.1 安装 bookdown
1. 安装软件
必须安装
选择安装
2. 配置环境
Step 1: Rstudio 配置
安装好 R 和 Rstudio 之后,开始着手进行软件配置.
点击桌面图标打开 Rstudio,找到Tools 菜单,下拉找到最后一项 Global options,点击打开如图1.1所示,在左边列表框中找到Sweave 选项,并按图中所示的最前面两处选择框按图示进行选择,然后点击下方 OK 按钮.
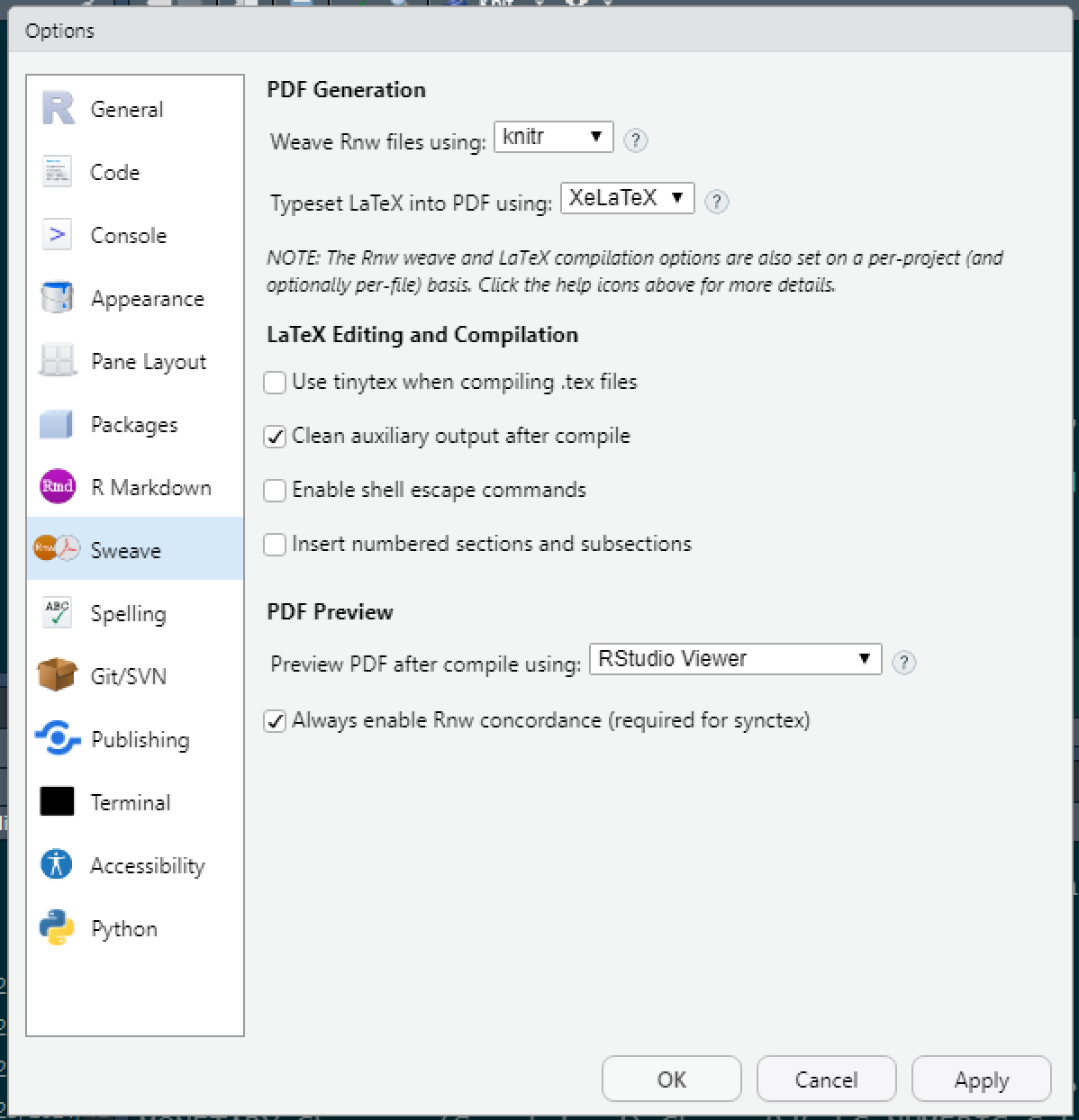
图 1.1: Rstudio 配置
Step 2: 安装 R 扩展包
安装所必须的三个 R 包: knitr、Rmarkdown、bookdown 以及 选装tinytex, 其它R扩展包根据工作的需要选择安装.
打开 Rstudio,按照下图1.2所示,找到 Package——install按钮并单击之
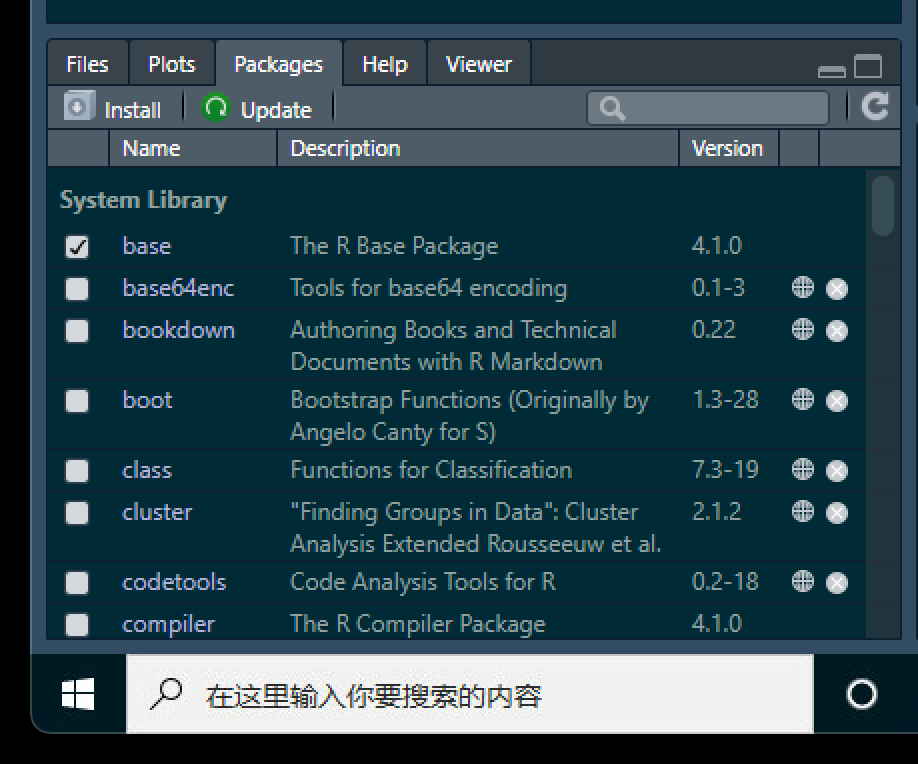
图 1.2: R 扩展包安装 1
单击 install 后,弹出如下对话框,在图中1.3光标处,分别输入上述四个扩展包的名字即可(随着字母输入,会看到下拉提示,选择即可).
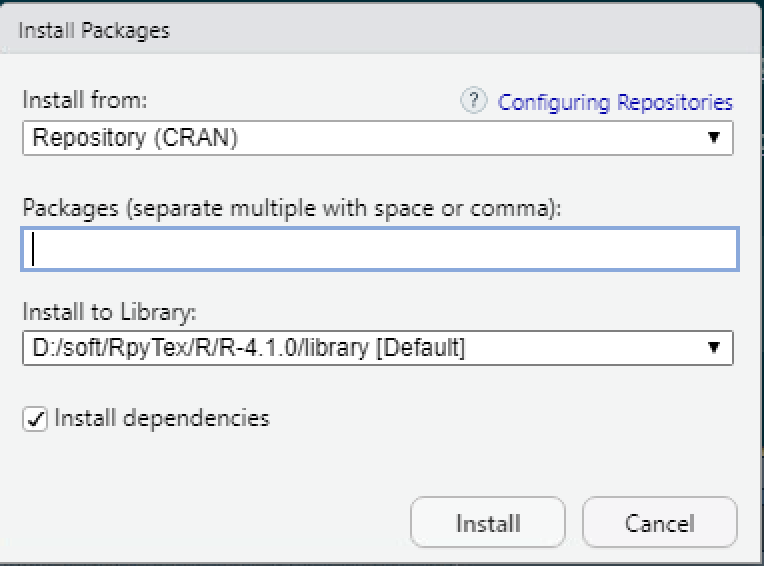
图 1.3: R 扩展包安装 2
注意:请务必选中左下 Install dependencies 前的复选框.
Stop 3:在 Rstudio 中安装定制的miniTex系统
如果需要生成 PDF 文档,则这一步很重要,否则,仅渲染 HTML可不安装.
即使在 Windows 中已经安装了 Ctex、Miktex、Texlive 等Latex系统,也要安装.安装方法是:
在 Rstudio 中,找到R终端控制台(即要有 R 的命令提示符” > “的窗口),这里是输入 R 命令的地方.
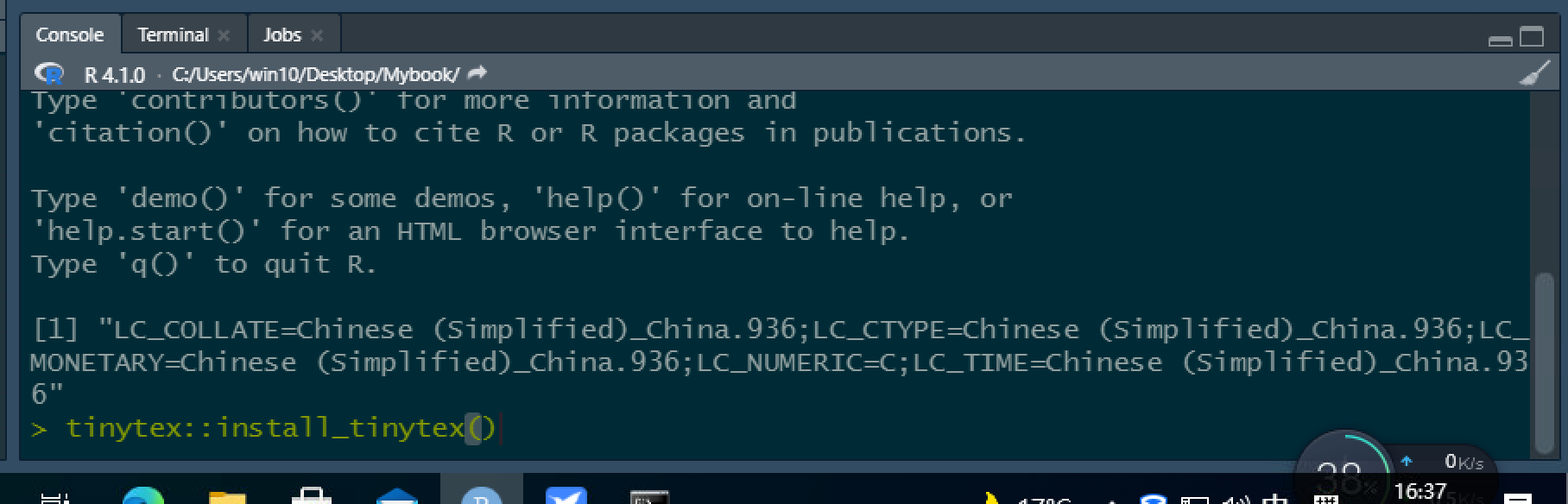
图 1.4: R 终端控制台
在 “>” 处输入:
>tinytex::install_tinytex()系统将从网络上实时下载、安装并配置一个定制的 Latex 系统,目前的版本大约有 99MB的容量;由于服务器所在地等原因,安装需要一些时间,安装过程也可能不稳定,请耐心等待.实在不行,试试下面的国内镜像
>tinytex::tlmgr_repo('http://mirrors.tuna.tsinghua.edu.cn/CTAN/')为了判断TinyTeX是否安装成功,安装提示完成后,在 “>” 处输入:
>tinytex::is_tinytex()结果为TRUE表示安装成功; 出错或者结果为FALSE都说明安装不成功,须重新安装直至成功.
安装成功之后,通常进行一次升级操作(以后也可以经常进行),方法是在 “>” 处输入:
>tlmgr_update()当用户使用rmarkdown、bookdown 等编译生成PDF文档时,如果缺少某些Latex宏包, tinytex会自动安装缺少的宏包,注意看运行提示信息.
关于 Tinytex ,详情请参考https://yihui.org/tinytex/cn/.
上述配置完成之后,请关闭并重新启动 Rstudio!
1.2 使用 bookdown
除了”用心耐心,熟能生巧”外,强调四点:
- 模版入手——研究并尝试改动,你会节省 99%的在黑暗中摸索的时间;瞬间,自信心和成就感爆棚!
- 遇到问题——要耐得住”寂寞”和”无奈”,一旦你有半夜爬起来调试代码的冲动,就离独立解决问题的时刻不远了!除此,请到”暗黑”的Rmarkdown cookbook、Rmarkdown和bookdown去潜水,你会摸到大鱼!
- 解决问题——独立尝试,不断试错,这是能力提升的最佳途径!
- 再遇到问题怎么办?——没办法了! 因为解决不了问题的人,本身就是问题!
1.3 常用典型环境
使用 bookdown 写作时可能用到的各种环境和模式,大部分在本项目章节源代码中都涉及到了;大家在动手写作前,务必对照渲染结果,认真研究源代码.
除此之外,还有一些可能用到的环境列举如下,供大家学习,以节省大家的宝贵时间.
1.3.1 数学环境
定理、证明和数学公式等数学环境是理工科写作经常用到的环境,以下是部分示例(源代码紧跟的是渲染后的结果),完整的说明见https://bookdown.org/yihui/bookdown/markdown-extensions-by-bookdown.html#theorems.
引理:
::: {.lemma #chf-pdf}
任意两个随机变量 $X_1$, $X_2$, 他们具有相同概率分布,当且仅当
$$\varphi _{X_1}(t)=\varphi _{X_2}(t)$$
:::引理 1.1 任意两个随机变量 \(X_1\), \(X_2\), 他们具有相同概率分布,当且仅当 \[\varphi _{X_1}(t)=\varphi _{X_2}(t)\]
定理:
::: {.theorem #chf-sum}
If $X_1$, ..., $X_n$ are independent random variables, and $a_1$, ..., $a_n$ are some constants, then the characteristic function of the linear combination $S_n=\sum_{i=1}^na_iX_i$ is
$$\varphi _{S_{n}}(t)=\prod_{i=1}^n\varphi _{X_i}(a_{i}t)=\varphi _{X_{1}}(a_{1}t)\cdots \varphi _{X_{n}}(a_{n}t)$$
:::定理 1.1 If \(X_1\), …, \(X_n\) are independent random variables, and \(a_1\), …, \(a_n\) are some constants, then the characteristic function of the linear combination \(S_n=\sum_{i=1}^na_iX_i\) is \[\varphi _{S_{n}}(t)=\prod_{i=1}^n\varphi _{X_i}(a_{i}t)=\varphi _{X_{1}}(a_{1}t)\cdots \varphi _{X_{n}}(a_{n}t)\]
命题:
::: {.proposition}
The distribution of the sum of independent Poisson random variables $X_i \sim \mathrm{Pois}(\lambda_i),\: i=1,2,\cdots,n$ is $\mathrm{Pois}(\sum_{i=1}^n\lambda_i)$.
:::命题 1.1 The distribution of the sum of independent Poisson random variables \(X_i \sim \mathrm{Pois}(\lambda_i),\: i=1,2,\cdots,n\) is \(\mathrm{Pois}(\sum_{i=1}^n\lambda_i)\).
证明:
::: {.proof}
The characteristic function of $X\sim\mathrm{Pois}(\lambda)$ is $\varphi _{X}(t)=e^{\lambda (e^{it}-1)}$. Let $P_n=\sum_{i=1}^nX_i$. We know from Theorem \@ref(thm:chf-sum) that
\begin{equation*}
\begin{split}
\varphi _{P_{n}}(t) & =\prod_{i=1}^n\varphi _{X_i}(t) \\
& =\prod_{i=1}^n e^{\lambda_i (e^{it}-1)} \\
& = e^{\sum_{i=1}^n \lambda_i (e^{it}-1)}
\end{split}
\end{equation*}
This is the characteristic function of a Poisson random variable with the parameter $\lambda=\sum_{i=1}^n \lambda_i$. From Lemma \@ref(lem:chf-pdf), we know the distribution of $P_n$ is $\mathrm{Pois}(\sum_{i=1}^n\lambda_i)$.
:::证明. The characteristic function of \(X\sim\mathrm{Pois}(\lambda)\) is \(\varphi _{X}(t)=e^{\lambda (e^{it}-1)}\). Let \(P_n=\sum_{i=1}^nX_i\). We know from Theorem 1.1 that \[\begin{equation*} \begin{split} \varphi _{P_{n}}(t) & =\prod_{i=1}^n\varphi _{X_i}(t) \\ & =\prod_{i=1}^n e^{\lambda_i (e^{it}-1)} \\ & = e^{\sum_{i=1}^n \lambda_i (e^{it}-1)} \end{split} \end{equation*}\] This is the characteristic function of a Poisson random variable with the parameter \(\lambda=\sum_{i=1}^n \lambda_i\). From Lemma 1.1, we know the distribution of \(P_n\) is \(\mathrm{Pois}(\sum_{i=1}^n\lambda_i)\).
注释:
::: {.remark}
In some cases, it is very convenient and easy to figure out the distribution of the sum of independent random variables using characteristic functions.
:::注. In some cases, it is very convenient and easy to figure out the distribution of the sum of independent random variables using characteristic functions.
推论:
::: {.corollary}
The characteristic function of the sum of two independent random variables $X_1$ and $X_2$ is the product of characteristic functions of $X_1$ and $X_2$, i.e.,
$$\varphi _{X_1+X_2}(t)=\varphi _{X_1}(t) \varphi _{X_2}(t)$$
:::推论 1.1 The characteristic function of the sum of two independent random variables \(X_1\) and \(X_2\) is the product of characteristic functions of \(X_1\) and \(X_2\), i.e., \[\varphi _{X_1+X_2}(t)=\varphi _{X_1}(t) \varphi _{X_2}(t)\]
练习:
::: {.exercise name="Characteristic Function of the Sample Mean"}
Let $\bar{X}=\sum_{i=1}^n \frac{1}{n} X_i$ be the sample mean of $n$ independent and identically distributed random variables, each with characteristic function $\varphi _{X}$. Compute the characteristic function of $\bar{X}$.
:::练习 1.1 (Characteristic Function of the Sample Mean) Let \(\bar{X}=\sum_{i=1}^n \frac{1}{n} X_i\) be the sample mean of \(n\) independent and identically distributed random variables, each with characteristic function \(\varphi _{X}\). Compute the characteristic function of \(\bar{X}\).
求解:
::: {.solution}
Applying Theorem \@ref(thm:chf-sum), we have
$$\varphi _{\bar{X}}(t)=\prod_{i=1}^n \varphi _{X_i}\left(\frac{t}{n}\right)=\left[\varphi _{X}\left(\frac{t}{n}\right)\right]^n.$$
:::解. Applying Theorem 1.1, we have \[\varphi _{\bar{X}}(t)=\prod_{i=1}^n \varphi _{X_i}\left(\frac{t}{n}\right)=\left[\varphi _{X}\left(\frac{t}{n}\right)\right]^n.\]
1.3.2 代码环境
独立代码块:显示包括代码块设置参数的代码块:
```{r, eval=TRUE}
1 + 1
```行内代码段:
- 情形 1:不显示而执行代码:
This will show a verbatim inline R expression 2 in the output.
- 情形 2:显示而不执行代码:
This will show a verbatim inline R expression`r 1+1` in the output.
1.3.3 图片环境
注意研究相关章节源代码进行图片的规范插入.
所谓规范是指用knitr::include_graphics()命令插入外部图片,不要使用 Markdown 的图片插入命令,因为兼容性不好,特别是转换为 PDF 时.
1.3.4 表格环境
- 表格数据来自内部数据:所谓内部数据是指以 R 的数据框 data.frame格式保存的数据文件.
表格1.1示例
d2 <- head(mtcars[, 1:3], 5)
colnames(d2)[3] <- "$\\Phi$"
knitr::kable(
d2,
align = "lccc",
caption = 'Single tables',
booktabs = TRUE, valign = 't'
)| mpg | cyl | \(\Phi\) | |
|---|---|---|---|
| Mazda RX4 | 21.0 | 6 | 160 |
| Mazda RX4 Wag | 21.0 | 6 | 160 |
| Datsun 710 | 22.8 | 4 | 108 |
| Hornet 4 Drive | 21.4 | 6 | 258 |
| Hornet Sportabout | 18.7 | 8 | 360 |
表格1.2 示例
d1 <- head(cars, 3)
d2 <- head(mtcars[, 1:3], 5)
rownames(d1) <- c("$\\beta_0$", "$\\beta_1$","$\\beta_2$")
colnames(d2)[3] <- "$\\Phi$"
knitr::kable(
list(d1, d2),
caption = 'Two tables placed side by side.',
booktabs = TRUE, valign = 't'
)
|
|
表格1.3 示例
knitr::kables(
list(
# the first kable() to change column names
knitr::kable(
d1, col.names = c('SPEED', 'DISTANCE'),valign = 't'
),
# the second kable() to set the digits option
knitr::kable(d2, digits = 0, valign = 't')
),
caption = 'Two tables created by knitr::kables().'
)
|
|
带标题的表格将被编号,并可以被引用. Kable ()函数将自动为表格生成一个标签.
- 表格数据来自外部数据:所谓文本数据是指以非 R的数据框
data.frame格式保存的数据文件.
此类数据生成表格的方法是:可以先将数据转化为 R 的数据框文件,再利用上面方法进行表格显示,具体可上网搜索转换方法.
1.3.5 提醒环境
下面是一个示例,除了示例的形式外,还可以有其他形式,细节请参见https://bookdown.org/yihui/rmarkdown-cookbook/custom-blocks.html.
NOTICE!
凡是能轻易诱惑你的,多不是好物;美好的东西常常深藏不露,而探求的历程又过于艰辛!
1.4 参考文献的生成
因生成方法不同,参考文献分为”引用R 包的参考文献”和”其它(书籍、文章、网络资源等)参考文献”两类,下面分别给出生成方法.
1.4.1 引用 R 包的参考文献生成方法
打开本项目(文件夹)内文件名为 31-ref.rmd 的文件,会看到如下内容:
```{r include=FALSE}
自动生成 R 包的参考文献
knitr::write_bib(c(
.packages(), 'bookdown', 'knitr', 'rmarkdown','tinytex'
), 'packages.bib')
```只需把你要引用的 R 包,按照上面代码显示的格式,正确地填入 R 包的名字即可. Build 之后, 引用 R 包的所需参考文献信息会自动生成并存入 packages.bib 文件(可查看本项目内的文件 packages.bib).
1.5 reticulate 之 Python配置
由于bookdown 是基于 R 和 Rstudio 由 Rmarkdown二次开发的写作环境,故对 R 语言的支持是十分完美的,但对其他语言的支持多少有些不够理想.
现在有了 reticulate 扩展包, 安装之后,在build渲染时,实现后台动态运行 python 代码,并把 Python 代码运行结果自动插入文中.也就是说,在写作过程中,实现了 R 和 Python 的混用.
更值得一提的是Python 和 R 之间可以双向进行变量、对象调用和通信,这是实乃天大之幸事!

图 1.5: Reticulate R & Python
但是,新手配置reticulate比较难于上手,这里简要说明一下:
- 运行 Python代码需要 R 扩展包 reticulate 支持,也即要安装 reticulate 扩展包
- 经测试(有待进一步确定),目前使用Python 语言,似乎仅支持 matplotlib 模块绘图,其它绘图模块如 seaborn 等不支持
- 需要指定 Python 运行的虚拟环境(目前,用于数据科学的最好的Python集成发行版是 Anaconda,请注意其版本不能太旧),参见模版index.rmd 文件的导言部分的最后三行:
# 以下是 python 环境配置
library(reticulate)
use_python("/Users/hbsun/opt/anaconda3/envs/r-reticulate/bin/python")
use_virtualenv("r-reticulate")但需要根据你的 anaconda 安装路径,对use_python中的路径进行必要的修改,注意路径中anaconda3/envs/r-reticulate/bin/python这一关键路径!!!
即:
use_python("改为你的计算机中包含关键路径的 Python 路径")至于需要的 Python 路径,方法之一是参考下图 anaconda 的界面,在r-reticulate环境标签点击三角符号,再点击Open with Python,在弹出的终端窗口就可以找到你需要的 python路径:
 其中的 r-reticulate环境应该是你安装 anaconda 后,第一次 build 时,安装程序自动为你建立的. 还须注意的是,今后如果在写作过程中需要使用 python,可能需要在
其中的 r-reticulate环境应该是你安装 anaconda 后,第一次 build 时,安装程序自动为你建立的. 还须注意的是,今后如果在写作过程中需要使用 python,可能需要在 r-reticulate 环境中安装必要的模块,虽然该模块在你的宿主环境base中已经安装.
1.6 发布作品到互联网
在编写过程中,您可以,可能也希望将书的草稿提供给公众,以获得读者的早期反馈.将其发布到互联网上是一种最便捷、最流行的做法.这里推荐两种比较简单的方法,连同其它更高深一些的技术,请参见此处学习.
- Rstudio Connect
通过 Rstudio Connect 把书稿上传到 Bookdown 图书馆,这是 RStudio 提供的一个免费托管你的书的网站.
这个网站建立在“ RStudio Connect”之上,这是一个 RStudio 产品,它允许你在服务器上部署各种与 r 相关的应用程序,包括 r Markdown 文档、 Shiny 应用程序、 r 绘图等等.
你不需要知道很多关于 RStudio Connect 的知识就可以把你的书发布到 bookdown.org.你只须在 bookdown注册,当你第一次尝试运行bookdown: : publish _ book ()时,你会被要求授权 bookdown 来发布到你的 bookdown.org 账户.今后,您只需再次调用publish _ book (),bookdown 将不再要求任何东西.
惟一的问题:你要有一个 Google 账户!
- Netlify Drop
Netlify是一个为静态网站提供云托管和无服务器后端服务的专业网站,提供免费和付费的服务.但是他们也提供了一个免费 Netlify Drop的服务,不需要 Netlify 帐号就可以使用,您只须一个可以在本地构建好的 bookdown 项目即可.
打开Netlify Drop,你会看到一个框,告诉你“Drag and Drop your site output folder here”.接下来,将你要发布的 bookdown 项目 的输出文件夹(默认情况下为_ book/,除非在_ bookdown.yml文件中将其更改)拖放到 web 浏览器中的那个框中.你应该看到你的书快速部署了一个随机的子域名,会给你一个类似下面的网址
https://random-word-12345.netlify.com.分享给其他人,其在浏览器中打开生成的网址,就可以看到你的作品了,非常简单方便! 但是非 Netlify 注册用户,该网址24小时后会实效.你可以注册一个 Netlify 帐户来认领你的网站,并让它永久在线.
惟一的期待:网络要给力!